base64

题目

难度系数： 1.0
题目来源： poxlove3
题目描述：元宵节灯谜是一种古老的传统民间观灯猜谜的习俗。 因为谜语能启迪智慧又饶有兴趣，灯谜增添节日气氛，是一项很有趣的活动。 你也很喜欢这个游戏，这不，今年元宵节，心里有个黑客梦的你，约上你青梅竹马的好伙伴小鱼， 来到了cyberpeace的攻防世界猜谜大会，也想着一展身手。 你们一起来到了小孩子叽叽喳喳吵吵闹闹的地方，你俩抬头一看，上面的大红灯笼上写着一些奇奇怪怪的 字符串，小鱼正纳闷呢，你神秘一笑，我知道这是什么了。

解答

根据题目提示用base64解密附件得到答案cyberpeace{Welcome_to_new_World!}。

Caesar47

题目

难度系数： 1.0
题目来源： poxlove3
题目描述：你成功的解出了来了灯谜，小鱼一脸的意想不到“没想到你懂得这么多啊！” 你心里面有点小得意，“那可不是，论学习我没你成绩好轮别的我知道的可不比你少，走我们去看看下一个” 你们继续走，看到前面也是热热闹闹的，同样的大红灯笼高高挂起，旁边呢好多人叽叽喳喳说个不停。你一看 大灯笼，上面还是一对字符，你正冥思苦想呢，小鱼神秘一笑，对你说道，我知道这个的答案是什么了

解密

根据题目提示，应该是凯撒密码，观察题目附件oknqdbqmoq{kag_tmhq_xqmdzqp_omqemd_qzodkbfuaz}，应该是偏移量为14，复原得到答案：cyberpeace{you_have_learned_caesar_encryption}。

Morse

题目

难度系数： 1.0
题目来源： poxlove3
题目描述：小鱼得意的瞟了你一眼，神神气气的拿走了答对谜语的奖励，你心里暗暗较劲 想着下一个谜题一定要比小鱼更快的解出来。不知不觉你们走到了下一个谜题的地方，这个地方有些奇怪。 上面没什么提示信息，只是刻着一些0和1，感觉有着一些奇怪的规律，你觉得有些熟悉，但是就是想不起来 这些01代表着什么意思。一旁的小鱼看你眉头紧锁的样子，扑哧一笑，对你讲“不好意思我又猜到答案了。”(flag格式为cyberpeace{xxxxxxxxxx},均为小写)

解答

根据附件的内容和题目提示，用摩斯密码解答，用-替换1，用.替换0，得到摩斯密码序列：

– — .-. … . -.-. — -… . … … … — … -. - . .-. . … - … -. --.

解密后得到答案morsecodeissointeresting。

幂数加密

题目

难度系数： 2.0
题目来源： CFF2016
题目描述：你和小鱼终于走到了最后的一个谜题所在的地方，上面写着一段话“亲爱的朋友， 很开心你对网络安全有这么大的兴趣，希望你一直坚持下去，不要放弃 ，学到一些知识， 走进广阔的安全大世界”，你和小鱼接过谜题，开始了耐心细致的解答。flag为cyberpeace{你解答出的八位大写字母}

解答

根据附件字符串8842101220480224404014224202480122，以及题目中的提示幂数加密,八位字母。
可以发现附件是用0分割的八个字符，每一段加起来之后得到数字23,5,12,12,4,15,14,5。对应英文字母位置得到答案为WELLDONE。

Railfence

题目

难度系数： 2.0
题目来源： poxlove3
题目描述：被小鱼一连将了两军，你心里更加不服气了。两个人一起继续往前走， 一路上杂耍卖艺的很多，但是你俩毫无兴趣，直直的就冲着下一个谜题的地方去了。 到了一看，这个谜面看起来就已经有点像答案了样子了，旁边还画着一张画，是一副农家小院的 图画，上面画着一个农妇在栅栏里面喂5只小鸡，你嘿嘿一笑对着小鱼说这次可是我先找到答案了。

解答

根据题亩名称和题干，考虑用栅栏密码解题，将附件字符串重新排列。

c c e h g  
y a e f n  
p e o o b   
e { l c i  
r g } e p  
r i e c _  
o r a _ g

得到字符串cyperrocae{gireeol}eahfocec_gnbip_g,发现并没有什么卵用。

百度之后发现还有一种WWW加密方式。

对于字符串：123456789
key=3
1----5----9 \让数字以W型组织，同样是三组，但每组的数量不一定相同
-2–4-6–8
–3----7–
加密密文：159246837

回到本题，已知第一个斜线应该构成cyberpeace等字样，可构造解密图形如下：

c       c       e       h       g  
 y     a e     f n     p e     o o  
  b   e   {   l   c   i   r   g   }    
   e p     r i     e c     _ o      
    r       a       _       g

得到解密后的字符串为cyberpeace{railfence_cipher_gogogo}

不仅仅是Morse

题目

难度系数：2.0
题目来源： poxlove3
题目描述：“这个题目和我们刚刚做的那个好像啊但是为什么按照刚刚的方法做出来答案却不对呢” ，你奇怪的问了问小鱼，“可能是因为还有一些奇怪的加密方式在里面吧，我们在仔细观察观察”。两个人 安安静静的坐下来开始思考，很耐心的把自己可以想到的加密方式一种种的过了一遍，十多分钟后两个人 异口同声的说“我想到了！”。一种食物,格式为cyberpeace{小写的你解出的答案}

解答

把题目附件先用莫斯密码解密，得到提示maybe have another decode和一串字符串，观察全部采用AB构成，考虑培根密码，分组如下：

aaaaa baabb baabb aaaaa aaaba ababa aaaaa abbab aaabb aaabb aabaa aabab aabaa abbab aaaba aabaa babba abbba baaab ababb aaabb abaaa baaba abaaa abbab baabb aabaa baaab aabaa baaba baabb abaaa abbab aabba

根据培根密码表，得到解密后的字符串ATTACKANDDEFENCEWORLDISINTERESTING。

混合编码

题目

难度系数： 2.0
题目来源： poxlove3
题目描述：经过了前面那么多题目的历练，耐心细致在解题当中是 必不可少的品质，刚巧你们都有，你和小鱼越来越入迷。那么走向了下一个题目，这个题目好长 好长，你知道你们只要细心细致，答案总会被你们做出来的，你们开始慢慢的尝试，慢慢的猜想 ，功夫不负有心人，在你们耐心的一步步的解答下，答案跃然纸上，你俩默契一笑，相视击掌 走向了下面的挑战。格式为cyberpeace{小写的你解出的答案}

解答

看到附件格式，首先想到用base64解密,解密得到：
LzExOS8xMDEvMTA4Lzk5LzExMS8xMDkvMTAxLzExNi8xMTEvOTcvMTE2LzExNi85Ny85OS8xMDcvOTcvMTEwLzEwMC8xMDAvMTAxLzEwMi8xMDEvMTEwLzk5LzEwMS8xMTkvMTExLzExNC8xMDgvMTAw

是HTML编码，再次解密得到：

LzExOS8xMDEvMTA4Lzk5LzExMS8xMDkvMTAxLzExNi8xMTEvOTcvMTE2LzExNi85Ny85OS8xMDcvOTcvMTEwLzEwMC8xMDAvMTAxLzEwMi8xMDEvMTEwLzk5LzEwMS8xMTkvMTExLzExNC8xMDgvMTAw

用Base64再次解码得到：

/119/101/108/99/111/109/101/116/111/97/116/116/97/99/107/97/110/100/100/101/102/101/110/99/101/119/111/114/108/100

转换为ASCII码得到答案：welcometoattackanddefenceworld。

easy_RSA

题目

难度系数： 3.0
题目来源： poxlove3
题目描述：解答出来了上一个题目的你现在可是春风得意，你们走向了下一个题目所处的地方 你一看这个题目傻眼了，这明明是一个数学题啊！！！可是你的数学并不好。扭头看向小鱼，小鱼哈哈一笑 ，让你在学校里面不好好听讲现在傻眼了吧~来我来！三下五除二，小鱼便把这个题目轻轻松松的搞定了。flag格式为cyberpeace{小写的你解出的答案}

解答

用Rsa Tool 2，注意Number Base要选10进制，然后E使用16进制表示的，10进制的17要转换成16进制的11，然后计算D值。

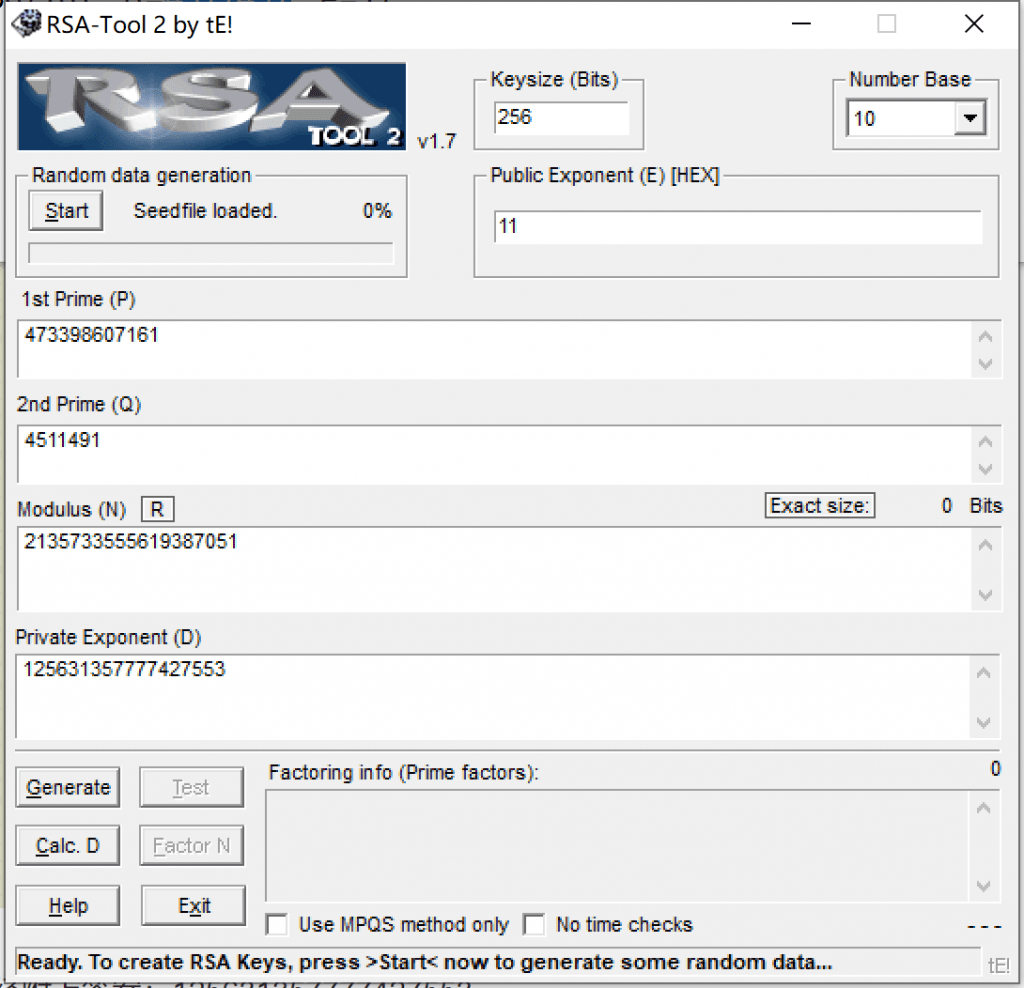
得到答案cyberpeace{125631357777427553}。

easychallenge

题目

难度系数： 3.0
题目来源： NJUPT_CTF
题目描述：你们走到了一个冷冷清清的谜题前面，小鱼看着题目给的信息束手无策，丈二和尚摸不着头脑 ，你嘿嘿一笑，拿出来了你随身带着的笔记本电脑，噼里啪啦的敲起来了键盘，清晰的函数逻辑和流程出现在 了电脑屏幕上，你敲敲键盘，更改了几处地方，运行以后答案变出现在了电脑屏幕上。

解答

逆向pyc文件，使用uncompyle6。

uncompyle6 -o . ctf.pyc。

得到逆向的py文件，代码如下：

import base64

def encode1(ans):
    s = ''
    for i in ans:
        x = ord(i) ^ 36
        x = x + 25
        s += chr(x)

    return s


def encode2(ans):
    s = ''
    for i in ans:
        x = ord(i) + 36
        x = x ^ 36
        s += chr(x)

    return s


def encode3(ans):
    return base64.b32encode(ans)


flag = ' '
print 'Please Input your flag:'
flag = raw_input()
final = 'UC7KOWVXWVNKNIC2XCXKHKK2W5NLBKNOUOSK3LNNVWW3E==='
if encode3(encode2(encode1(flag))) == final:
    print 'correct'
else:
    print 'wrong'

可以看出正确的flag应该是经过三个函数加密后与final字符串相等，所以只需要将final作为输入，经过三次相反的解密过程就可以得到正确的flag，这里我用的是python3，所以做了一些兼容性的修改。

import base64


def encode1(ans):
    s = ''
    for i in ans:
        x = ord(i) ^ 36
        x = x + 25
        s += chr(x)

    return s


def decode1(ans):
    s = ''
    for i in ans:
        x = ord(i) - 25
        x = x ^ 36
        s += chr(x)
    return s


def encode2(ans):
    s = ''
    for i in ans:
        x = ord(i) + 36
        x = x ^ 36
        s += chr(x)

    return s


def decode2(ans):
    s = ''
    for i in ans:
        x = ord(i) ^ 36
        x = x - 36
        s += chr(x)
    return s


def encode3(ans):
    return base64.b32encode(ans)


def decode3(ans):
    return base64.b32decode(ans)


# flag = ' '
# print('Please Input your flag:')
# flag = input()
final = 'UC7KOWVXWVNKNIC2XCXKHKK2W5NLBKNOUOSK3LNNVWW3E==='
flag = decode1(decode2(decode3(final).decode('ISO-8859-1')))
print(flag)
# if encode3(encode2(encode1(flag))) == final:
#     print('correct')
# else:
#     print('wrong')

这里这个decode选项ISO-8859-1我也不知道是为什么，尝试了utf-8和unicode-escape之类的全部是乱码无法解析，只有这个才能正常显示答案：cyberpeace{interestinghhhhh}。

转轮机加密

题目

难度系数： 4.0
题目来源： ISCC2017
题目描述：你俩继续往前走，来到了前面的下一个关卡，这个铺面墙上写了好多奇奇怪怪的 英文字母，排列的的整整齐齐，店面前面还有一个大大的类似于土耳其旋转烤肉的架子，上面一圈圈的 也刻着很多英文字母，你是一个小历史迷，对于二战时候的历史刚好特别熟悉，一拍大腿：“嗨呀！我知道 是什么东西了！”。提示：托马斯·杰斐逊。 flag，是字符串，小写。

解答

根据秘钥的顺序决定轮子的顺序，根据密文的字母决定每一个轮子的重新排列。
对于原文：

< ZWAXJGDLUBVIQHKYPNTCRMOSFE <  
< KPBELNACZDTRXMJQOYHGVSFUWI <  
< BDMAIZVRNSJUWFHTEQGYXPLOCK <  
< RPLNDVHGFCUKTEBSXQYIZMJWAO <  
< IHFRLABEUOTSGJVDKCPMNZQWXY <  
< AMKGHIWPNYCJBFZDRUSLOQXVET <  
< GWTHSPYBXIZULVKMRAFDCEONJQ <  
< NOZUTWDCVRJLXKISEFAPMYGHBQ <  
< XPLTDSRFHENYVUBMCQWAOIKZGJ <  
< UDNAJFBOWTGVRSCZQKELMXYIHP <  
< MNBVCXZQWERTPOIUYALSKDJFHG <    
< LVNCMXZPQOWEIURYTASBKJDFHG <  
< JZQAWSXCDERFVBGTYHNUMKILOP <  

根据秘钥：

密钥为：2,3,7,5,13,12,9,1,8,10,4,11,6
密文为： N F Q K S E V O Q O F N P

进行重新排列后可以得到一个通顺的单词就是答案：

< NACZDTRXMJQOYHGVS F UWIKPBEL <   
< FHTEQGYXPLOCKBDMA I ZVRNSJUW <   
< QGWTHSPYBXIZULVKM R AFDCEONJ <  
< KCPMNZQWXYIHFRLAB E UOTSGJVD <   
< SXCDERFVBGTYHNUMK I LOPJZQAW <  
< EIURYTASBKJDFHGLV N CMXZPQOW <   
< VUBMCQWAOIKZGJXPL T DSRFHENY <  
< OSFEZWAXJGDLUBVIQ H KYPNTCRM <  
< QNOZUTWDCVRJLXKIS E FAPMYGHB <  
< OWTGVRSCZQKELMXYI H PUDNAJFB <   
< FCUKTEBSXQYIZMJWA O RPLNDVHG <    
< NBVCXZQWERTPOIUYA L SKDJFHGM <   
< PNYCJBFZDRUSLOQXV E TAMKGHIW < 

Normal_RSA

题目

难度系数： 5.0
题目来源： PCTF
题目描述：你和小鱼走啊走走啊走，走到下一个题目一看你又一愣，怎么还是一个数学题啊 小鱼又一笑，hhhh数学在密码学里面很重要的！现在知道吃亏了吧！你哼一声不服气，我知道数学 很重要了！但是工具也很重要的，你看我拿工具把他解出来！你打开电脑折腾了一会还真的把答案 做了出来，小鱼有些吃惊，向你投过来一个赞叹的目光

解答

附件是enc和pem文件，先用openssl解析public.pem

OpenSSL> rsa -pubin -text -modulus -in warmup -in pubkey.pem
RSA Public-Key: (256 bit)
Modulus:
    00:c2:63:6a:e5:c3:d8:e4:3f:fb:97:ab:09:02:8f:
    1a:ac:6c:0b:f6:cd:3d:70:eb:ca:28:1b:ff:e9:7f:
    be:30:dd
Exponent: 65537 (0x10001)
Modulus=C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD
writing RSA key
-----BEGIN PUBLIC KEY-----
MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMJjauXD2OQ/+5erCQKPGqxsC/bNPXDr
yigb/+l/vjDdAgMBAAE=
-----END PUBLIC KEY-----
OpenSSL>

得到E是65537，N是C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD。

把16进制的N转为10进制得到87924348264132406875276140514499937145050893665602592992418171647042491658461。

通过大素数在线分解得到p和q分别为 275127860351348928173285174381581152299和319576316814478949870590164193048041239。

后面的代码我没跑起来，总是报错，这里是复制网上的：

使用rsatool，输入命令以下命令生成private.pem文件。

python rsatool.py -f PEM -o private.pem -p 275127860351348928173285174381581152299 -q 319576316814478949870590164193048041239 -e 65537

然后把private.pem和pubkey.pem、flag.enc放一个文件夹里，打开cmder，使用openssl用private.pem解密flag.enc文件并将明文生成txt文件

输入命令：

rsautl -decrypt -in flag.enc -inkey private.pem -out flag.txt

成功生成flag.txt，得到答案PCTF{256b_i5_m3dium}。

easy_ECC

题目

难度系数： 6.0
题目来源： XUSTCTF2016
题目描述：转眼两个人又走到了下一个谜题的地方，这又是一种经典的密码学加密方式 而你刚好没有这个的工具，你对小鱼说“小鱼我知道数学真的很重要了，有了工具只是方便我们使用 懂了原理才能做到，小鱼你教我一下这个缇努怎么做吧！”在小鱼的一步步带领下，你终于明白了ECC 的基本原理，成功的解开了这个题目，两个人相视一笑，快步走向了下一个题目所在的位置。flag格式为cyberpeace{x+y的值}

解答

并不会做，看都看不懂，抄的代码。

import collections


def inverse_mod(k, p):
    """Returns the inverse of k modulo p.
   This function returns the only integer x such that (x * k) % p == 1.
   k must be non-zero and p must be a prime.
   """
    if k == 0:
        raise ZeroDivisionError('division by zero')

    if k < 0:
        # k ** -1 = p - (-k) ** -1 (mod p)
        return p - inverse_mod(-k, p)

    # Extended Euclidean algorithm.
    s, old_s = 0, 1
    t, old_t = 1, 0
    r, old_r = p, k

    while r != 0:
        quotient = old_r // r
        old_r, r = r, old_r - quotient * r
        old_s, s = s, old_s - quotient * s
        old_t, t = t, old_t - quotient * t

    gcd, x, y = old_r, old_s, old_t

    assert gcd == 1
    assert (k * x) % p == 1

    return x % p


# Functions that work on curve points #########################################

def is_on_curve(point):
    """Returns True if the given point lies on the elliptic curve."""
    if point is None:
        # None represents the point at infinity.
        return True

    x, y = point

    return (y * y - x * x * x - curve.a * x - curve.b) % curve.p == 0


def point_neg(point):
    """Returns -point."""
    assert is_on_curve(point)

    if point is None:
        # -0 = 0
        return None

    x, y = point
    result = (x, -y % curve.p)

    assert is_on_curve(result)

    return result


def point_add(point1, point2):
    """Returns the result of point1 + point2 according to the group law."""
    assert is_on_curve(point1)
    assert is_on_curve(point2)

    if point1 is None:
        # 0 + point2 = point2
        return point2
    if point2 is None:
        # point1 + 0 = point1
        return point1

    x1, y1 = point1
    x2, y2 = point2

    if x1 == x2 and y1 != y2:
        # point1 + (-point1) = 0
        return None

    if x1 == x2:
        # This is the case point1 == point2.
        m = (3 * x1 * x1 + curve.a) * inverse_mod(2 * y1, curve.p)
    else:
        # This is the case point1 != point2.
        m = (y1 - y2) * inverse_mod(x1 - x2, curve.p)

    x3 = m * m - x1 - x2
    y3 = y1 + m * (x3 - x1)
    result = (x3 % curve.p,
              -y3 % curve.p)

    assert is_on_curve(result)

    return result


def scalar_mult(k, point):
    """Returns k * point computed using the double and point_add algorithm."""
    assert is_on_curve(point)

    if k < 0:
        # k * point = -k * (-point)
        return scalar_mult(-k, point_neg(point))

    result = None
    addend = point

    while k:
        if k & 1:
            # Add.
            result = point_add(result, addend)

        # Double.
        addend = point_add(addend, addend)

        k >>= 1

    assert is_on_curve(result)

    return result


# Keypair generation and ECDHE ################################################

def make_keypair():
    """Generates a random private-public key pair."""
    private_key = curve.n
    public_key = scalar_mult(private_key, curve.g)

    return private_key, public_key


EllipticCurve = collections.namedtuple('EllipticCurve', 'name p a b g n h')
curve = EllipticCurve(
    'secp256k1',
    # Field characteristic.
    p=15424654874903,
    # Curve coefficients.
    a=16546484,
    b=4548674875,
    # Base point.
    g=(6478678675, 5636379357093),
    # Subgroup order.
    n=546768,
    # Subgroup cofactor.
    h=1,
)
private_key, public_key = make_keypair()
print("private key:", hex(private_key))
print("public key: (0x{:x}, 0x{:x})".format(*public_key))
print("x + y = " + str(public_key[0] + public_key[1]))

结果：

private key: 0x857d0
public key: (0xcb19fe553fa, 0x50545408eb4)
x + y = 19477226185390